A Short History of Positional Encoding

Since I first saw the ‘Attention Is All You Need’ paper, I had a strong curiosity about the principle and theory of positional encoding. It is well understood that the Transformer did not have inductive biases for RNN architectures and thus introduced positional encoding. However, I have still not convinced how and why this works. The authors mentioned that they chose this design because of the special nature of sinusoid about the relative position, but it was not enough for me.

… we hypothesized it would allow the model to easily learn to attend by relative positions, since for any fixed offset $k$, $PE_{pos+k}$ can be represented as a linear function of $PE_{pos}$. (Section 3.5 in Vaswani et al., 2017)

While searching related literature, I was able to read the papers to develop more advanced positional encoding. In particular, I found that positional encoding in Transformer can be beautifully extended to represent the time (generalization to the continuous space) and positions in a graph (generalization to the irregular structure). In this post, I review the work related to positional encoding and describe what theories are based on the generalization to time and graph.

Positional Representation

Learned Positional Embedding

Prior Transformers, Gehring et al., 2017 (ConvS2S) replaces recurrent neural networks with convolutional neural networks for the sequence to sequence learning. It might be less effective than attention-only-modules, but convolution is able to exploit the parallelism of GPU hardware rather than recurrent units. Since the convolution operator only sees the sequence’s part, it can only learn the word orders within kernel size and not the whole context. That is why ConvS2S uses additional embedding to let the model know the input’s position.

Its implementation is straightforward. Positional embedding in ConvS2S is a just learnable parameter with the same dimension of the word embedding.

# https://github.com/pytorch/fairseq/blob/master/fairseq/modules/positional_embedding.py#L25-L26
m = LearnedPositionalEmbedding(num_embeddings, embedding_dim, padding_idx)
nn.init.normal_(m.weight, mean=0, std=embedding_dim ** -0.5)

Vaswani et al., 2017 (Transformer) compares ConvS2S’ learned positional embedding and their sinusoidal embedding, and the performances are almost the same. It also argues that “sinusoidal version may allow the model to extrapolate to sequence lengths longer than the ones encountered during training”.

Positional Encoding with Sinusoids

As we can see from the title, Attention Is All You Need, Transformers fully replace the recurrent units with attention. Unlike the recurrent unit, the attention computation across tokens can be fully parallelized, that is, they do not have to wait for the calculation of the previous token’s representation to get the current token’s representation. However, in return for the grace of parallelization, Transformers gave up the inductive bias of recurrence that RNNs have. Without positional encoding, the Transformer is permutation-invariant as an operation on sets. For example, “Alice follows Bob” and “Bob follows Alice” are completely different sentences, but a Transformer without position information will produce the same representation. Therefore, the Transformer explicitly encodes the position information.

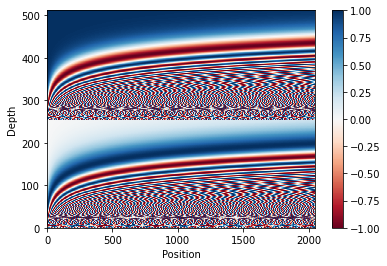
Their proposed sinusoidal positional encoding is probably the most famous variant of positional encoding in transformer-like models. These are composed of sine and cosine values with position index as input.

If we draw this equation, it looks like Figure 1.

Source: TensorFlow tutorial: Transformer model for language understanding

Relative Positional Encoding

Shaw et al., 2018, Dai et al., 2019 (Transformer-XL)

Learning to Encode Position for Transformer with Continuous Dynamical Model

Liu et al., 2020 (FLOATER)

Rethinking Positional Encoding

Ke et al., 2021

Generalization Beyond Position

Time Representation

Xu et al., 2019 (Bochner/Mercer Time Embedding), Kazemi et al., 2019 (time2vec), Voelker et al., 2019 (Legendre Memory Units) Xu et al., 2021 (Temporal Kernel), Shukla and Marlin, 2021 (Multi-time attention)

Tree Positional Encoding

Shiv and Quirk, 2019

Graph Positional Encodings with Laplacian Eigenvectors

Qiu et al., 2020 (GCC), Dwivedi et al., 2020 (Benchmarking GNNs)