Analytic Expressions of Indices for the Upper-triangle Matrix

Recently, I implemented the negative edge sampling of undirected graphs for PyTorch Geometric. Since $(i, j)$ and $(j, i)$ are the same edge in the undirected graph, I sample entries from the upper triangle of the given adjacency matrix. Easy solution is using numpy.triu_indices, but this suffers from $O(N^2)$ memory complexity (for $G = (V, E)$ and $N = |V|$) from the possible edge space $V \times V$.

For the negative sampling of directed graphs, the existing code of PyTorch Geometric first converts the coordinates $(i, j)$ to linear (or consecutive) indices $N \cdot i + j$ and samples indices from $[ 0, N^2 - 1 ]$ (range(N ** 2)). Note that using python standard random.sample with range is really memory-efficient as the docs says.

In order to apply this to the undirected version of negative sampling, we need to convert the upper triangle matrix into linear indices. For example, the linear indices of the $N = 4$ graph’s upper triangle matrix will be:

0  1  2  3
-  4  5  6
-  -  7  8
-  -  -  9

Encoding the coordinate $(i, j)$ to the linear index $X$ is straightforward. The cumulative number of neglected entries for the $i$th row is $\sum_{x=0}^{i} x = \frac{i (i + 1)}{2}$, so substracting this value to the indices of the original matrix will be the solution.

$X = Ni + j - \frac{i (i + 1)}{2}$.

What about the inverse? Can we infer $i$ and $j$ from $X$? The answer is yes. There are analytic expressions of $i$ and $j$ in terms of $X$, and actually are well known results in StackOverflow [1, 2].

$i = N - 1 - \left[\frac{-1 + \sqrt{(2N+1)^2 - 8 (X + 1)}}{2} \right]$

$j = X - Ni + \frac{i (i + 1)}{2}$

i = N - 1 - np.floor((-1 + np.sqrt((2 * N + 1) ** 2 - 8 * (X + 1))) / 2)
j = X - i * (2 * N - i - 1) // 2

My sincere friend, Chaehwan Song, explained to me how the above equations are derived. With her permission, I describe her solution in this post.

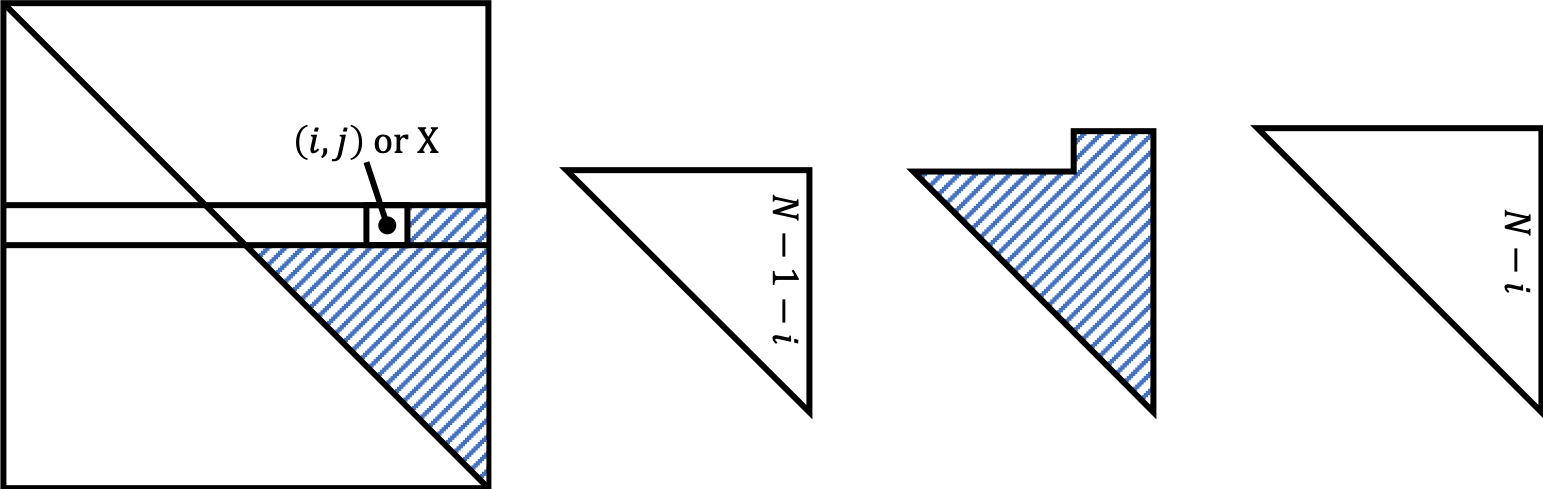
The size of the shaded area is $\sum_{z=1}^{N} z - (X + 1) = \frac{N(N+1)}{2} - (X + 1)$, and from the right figure, we know that the following equation holds.

$\sum_{z=1}^{N - 1 - i} z \leq \frac{N(N+1)}{2} - (X + 1) < \sum_{z=1}^{N - i} z$

$\Rightarrow \frac{(N-1-i)(N-i)}{2} \leq \frac{N(N+1)}{2} - (X + 1) < \frac{(N-i)(N-i+1)}{2}$ (①)

Let $i^c = N - 1 - i$ (for simplicity), $f(x) = \frac{x(x+1)}{2}$, and $k \in [0, N]$ s.t. $f(k) = \frac{N(N+1)}{2} - X$.

Then, equation ① becomes $f(i^c) \leq f(k) < f(i^c + 1)$.

Since $f(x)$ is monotically increasing at $[0, N]$, we obatin $i^c \leq k < i^c + 1$, which directly implies that $[ k ] = i^c$ holds (②).

From the definition of $k$,

$f(k) = \frac{k(k+1)}{2} = \frac{N(N+1)}{2} - (X + 1)$

$\Rightarrow k = \frac{-1 \pm \sqrt{(2N+1)^2 - 8 (X + 1)}}{2}$,

and proper $k \in [0, N]$ is $k = \frac{-1 + \sqrt{(2N+1)^2 - 8 (X + 1)}}{2}$.

From ②, we have $i^c = \left[ \frac{-1 + \sqrt{(2N+1)^2 - 8 (X + 1)}}{2} \right]$.

$\therefore i = N - 1 - \left[\frac{-1 + \sqrt{(2N+1)^2 - 8 (X + 1)}}{2} \right]$,

and $j$ follows in a straightforward way.